Un meccanismo particolare relativo all’evolversi dei tempi è la velocità con cui si manifestano fenomeni importanti, che raramente è lineare e regolare, molto più spesso è una crescita con velocità di tipo esponenziale.
L’esempio più semplice di crescita esponenziale si ha con “la leggenda della scacchiera e dei chicchi di grano”, dove il sovrano che volle premiare il servitore disse a questo di chiedere ciò che desiderasse. Egli chiese una cosa apparentemente modesta, cioè un chicco di grano sulla prima casella di una scacchiera, due sulla seconda, quattro sulla terza, otto sulla quarta, e così via. Pare che fu impossibile soddisfare la richiesta perché non sarebbero bastati i granai della terra.
Un altro esempio abbastanza comune è un sottilissimo foglio di carta immaginario, il quale piegato in due per 64 volte formerebbe una massa in grado di coprire la distanza tra la terra e la luna.
L’uomo pare non sia in grado di capire questo tipo di crescita esponenziale. Ci arriviamo con un ragionamento matematico senza riuscire a percepirlo con i nostri sensi. Numeri e azioni apparentemente semplici che si rivelano di grande impatto, ma comunque nulla di spettacolare di fronte ai prossimi esempi, avvenimenti quotidiani di cui non si è coscienti ma che incidono pesantemente sulla vita, l’economia, la socialità…
Il cambiamento esponenziale
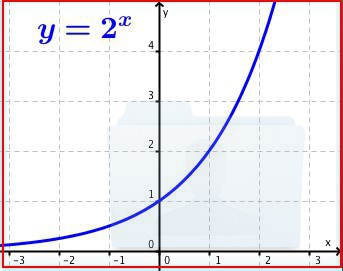
Cosa significa in pratica esponenziale? La nostra comprensione del mondo è lineare, mentre la realtà in molti casi segue dinamiche esponenziali che ci lasciano spiazzati. Trenta passi lineari fanno trenta passi, ma trenta passi esponenziali fanno un miliardo di passi. Il meccanismo si svela in questa formula che segue. Da un punto di vista matematico la crescita lineare si ha quando ogni termine, dal secondo in poi, si ottiene sommando una quantità costante. La crescita esponenziale si ha quando ogni termine, dal secondo in poi, si ottiene moltiplicando una quantità costante.
Quando una certa quantità viene sommata ad un’altra usiamo il segno ‘più’, il risultato è una crescita lineare e di solito riusciamo a prevedere cosa succederà. Se voglio riempire un contenitore da mezzo litro aggiungendo due gocce d’acqua al minuto, posso prevedere che dopo quattro ore sarà pieno.
Lo scenario cambia radicalmente quando al ‘più’ si sostituisce il segno ‘per’. Immaginando che lo stadio di San Siro sia utilizzato come vasca, se lo volessi riempire con un contagocce che raddoppia esponenzialmente ad ogni passaggio lo stesso contenuto raggiunto attualmente nello stadio del numero di gocce ogni minuto (uso il segno ‘per’ due, invece di ‘più’ due), quanto tempo ci vorrà per riempirlo tutto? La risposta è lontana dalla nostra comprensione: bastano circa 49 minuti. La cosa ancora più difficile da digerire è che fino al minuto 42 la quantità di acqua sarà trascurabile e lo stadio sarà vuoto al 99%. Infatti, quando siamo all’1% di riempimento, con un raddoppio ogni minuto, bastano 7 minuti per andare oltre il 100%. Questa è la realtà esponenziale che stiamo vivendo in molte attività quotidiane.
Esempio dei batteri nella bottiglia
 Il seguente esempio è proposto dal professor Bartlett, ed è davvero esplicativo della potenza del meccanismo del raddoppio. Serve inoltre a mostrare quanto la nostra mente non sia abituata a ragionare in termini esponenziali:
Il seguente esempio è proposto dal professor Bartlett, ed è davvero esplicativo della potenza del meccanismo del raddoppio. Serve inoltre a mostrare quanto la nostra mente non sia abituata a ragionare in termini esponenziali:
Immaginate di possedere una bottiglia contenente un certo numero di batteri. Tali batteri si moltiplicano con un tempo di raddoppio pari ad un minuto, cioè ogni minuto il numero di batteri raddoppia. Immaginate che il numero iniziale di batteri, alle 11, sia tale che, dopo un’ora, cioè alle 12, la bottiglia sia piena di batteri fino all’orlo. Il numero iniziale di batteri non è importante per questo esempio. Detto questo, proviamo a rispondere alle seguenti tre domande;
- Prima domanda: dopo quanto tempo il contenitore sarà pieno a metà? La risposta è semplice: alle 11.59, cioè un minuto prima delle 12. Infatti, visto che ogni minuto il numero di batteri raddoppia, un minuto prima delle 12 (ora in cui la bottiglia è piena) il numero di batteri sarà tale da riempire mezza bottiglia.
- Seconda domanda: immaginate di essere uno dei batteri presenti nella bottiglia, dopo quanto tempo pensate che riuscireste ad accorgervi che state per finire lo spazio a disposizione? In effetti la risposta a questa domanda è la base per capire come mai la crescita esponenziale porti al superamento dei limiti. Un minuto prima delle 12 la bottiglia sarà piena solo a metà. Due minuti prima delle 12 sarà piena per un quarto. Tre minuti prima delle 12 sarà piena per un ottavo. Quattro minuti prima delle 12 sarà piena per un sedicesimo e cinque minuti prima delle 12 sarà piena soltanto per un trentaduesimo. Pensate che sareste in grado di accorgervi che sta per finire lo spazio 6 minuti prima delle 12? Sebbene la crescita sia iniziata circa un’ora prima, 5 minuti prima di superare il limite la bottiglia è piena soltanto per un trentaduesimo.
- Terza domanda: immaginate che uno dei batteri si accorga che sta per finire lo spazio a disposizione e avverta gli altri e che insieme organizzino una spedizione fuori dalla bottiglia per cercare nuovi contenitori. Supponiamo che ne trovino tre completamente vuoti, più spazio di quanto abbiano mai avuto dall’inizio dei tempi. La domanda è: dopo quanti minuti anche queste tre nuove bottiglie sarebbero piene di batteri? La risposta è sorprendente: 2 minuti dopo le 12. In effetti alle 12 la prima bottiglia è piena. Alle 12.01 (raddoppio) due bottiglie sono piene. Alle 12.02 (raddoppio) tutti e quattro i contenitori sono stati riempiti.
Tutti iniziato con dei minuscoli batteri e poi improvvisamente: Fine dei giochi.
I miliardi come risultato esponenziale
Se pensiamo a come hanno vissuto i nostri avi nella prima metà del secolo scorso, fondamentalmente la loro vita era uguale a quella delle precedenti 100 generazioni. Ci si spostava di pochi chilometri in tutta la vita e si leggevano poche pagine – o nessuna prima di Gutenberg e l’invenzione della stampa. Si mangiava sempre lo stesso cibo coltivato a pochi chilometri da casa. Ci si addormentava col buio e ci si svegliava col sole. La stragrande maggioranza delle risorse umane era dedicata a produrre cibo. Si conoscevano poche decine di persone e le poche idee dominanti erano relativamente chiare e condivise. Nelle ultime due o tre generazioni abbiamo visto tutto questo cambiare radicalmente.
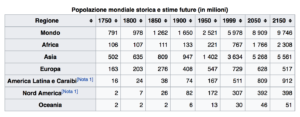 Se nell’anno 1750 avevamo raggiunto il mirabile numero di 791 milioni di esseri umani sul pianeta, già nel 1800 eravamo 978 milioni, ossia in 50 anni circa 190 milioni di anime in più. Nell’anno 1850 eravamo già un miliardo e 200 milioni, circa 250 milioni in più e sempre in 50 anni. Nel 1900 eravamo un miliardo 650 milioni, ossia 450 milioni in più in 50 anni.
Se nell’anno 1750 avevamo raggiunto il mirabile numero di 791 milioni di esseri umani sul pianeta, già nel 1800 eravamo 978 milioni, ossia in 50 anni circa 190 milioni di anime in più. Nell’anno 1850 eravamo già un miliardo e 200 milioni, circa 250 milioni in più e sempre in 50 anni. Nel 1900 eravamo un miliardo 650 milioni, ossia 450 milioni in più in 50 anni.
Arriviamo ad un più vicino 1950 con due miliardi e mezzo di umani sul pianeta, circa un miliardo di persone in più nello stesso lasso di tempo.
Nel 1970 eravamo oltre 4 miliardi, in soli venti anni siamo quasi raddoppiati e nell’anno 2000 eravamo 6 miliardi. Quasi triplicati nello stesso tempo di 50 anni.
Oggi, anno 2017, sul pianeta siamo quasi 7 miliardi e 600 milioni di anime abbastanza inconsapevoli di tutti gli altri.
Si stima che nell’anno 2050 saremo quasi 9 miliardi invece dei 14 miliardi previsti [grazie al freno dell’economia e di cos’altro si inventerà la creme dell’intellighenzia mondiale].
Ecco l’esponenziale: una certa cosa si modifica in maniera lentissima, quasi impercettibile per decenni e poi, di colpo, esplode. Si stima che il nostro cervello raddoppi la propria capacità di elaborare informazioni ogni 750.000 anni. Ma la quantità di informazioni disponibili sul pianeta, ai ritmi del 2010, raddoppia in 10 mesi. La legge che governa questo processo è quella di Moore, Intelligenza artificiale, robotica, Biotech, Nanotech, Information, sono alcune delle tecnologie che stanno crescendo esponenzialmente, il che presenta opportunità e rischi.
L’esponenzialità applicata agli esseri umani è improvvisamente diventata come il contenitore di batteri iniziale, ossia la presa di coscienza della sovrappopolazione.
Spero sia chiaro che il rischio più grande per la specie umana è la non comprensione della funzione esponenziale, come può esserlo una valanga per uno sciatore solitario.
Per avvicinarsi alla conclusione, proviamo un piccolo calcolo lineare su un risultato esponenziale.
Ipotizziamo di voler parlare con ogni essere umano presente sulla terra.
Dedichiamo un solo minuto a ciascuno dei 7,6 miliardi di persone, impiegheremmo quanto?
Nessun essere umano normale penserebbe mai ad una cosa del genere.
Proprio per questo il risultato del calcolo è incredibile per tutti.
7.600.000.000 persone-minuto / 60 minuti in un ora = 126.666.666,66 ore
126.666.666,66 ore / 24 ore di un giorno = 5.277.777,77 giorni
5.277.777,77 giorni / 365 giorni di un anno = 14.459,66 anni.
Sono più di 14 mila anni…
Premessa la situazione sociale del nostro pianeta, vorrei riportare alcuni ultimi esempi per aiutare a capire questo valore che sentiamo continuare a ripetere dai media ma che è evidente come non sia per noi minimamente comprensibile. Il Miliardo di Euro e i Miliardi di Stelle, ma anche Stelle in un altra versione.
Applicate questa realtà per quanto possibile all’economia, all’euro, alla crisi e al nostro quotidiano, ai rifiuti o all’inquinamento, ma anche al caso eccezionale della pandemia da virus, per capire quanto effettivamente sia potente un valore esponenziale.
Allego questa immagine per chiarire cosa avviene in caso di pandemia e cosa invece potrebbe accadere se la nostra mentre contemplasse l’esponenzialità.

Views: 395

Pingback: Organismi e cellule pro OGM • cartella di Stefano Monti
Pingback: Universo: Scienza e Religione • cartella di Stefano Monti
Pingback: Consumismo
Pingback: Vogliamo tutto senza in realtà ottenere poi niente
Pingback: Etica Pubblica: più confusi che persuasi, diceva Camilleri
Pingback: Con urgenza identità digitale cercasi!
Pingback: Umanità, evoluzione, intelligenza e artificialità; Parte 1: destino e natura umana
Pingback: Umanità, evoluzione, intelligenza e artificialità; Parte 3: perché progettiamo IA
Pingback: la regola del terzo cateto